 |
||||||||||||||||||||||||||||||||||||||||||
|
7. Cartesian coordinates in three dimensions
|
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
We begin with two dimensions. We have the following picture illustrating how to construct the Cartesian form of a point Q in the XOY plane. 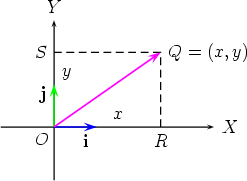
Vectors i and j are vectors of length 1 in the directions OX and OY respectively. The vector 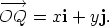 We now extend this to three dimensions to show how to construct the Cartesian form of a point P. Define k to be a vector of length 1 in the direction of OZ. We now have the following picture. 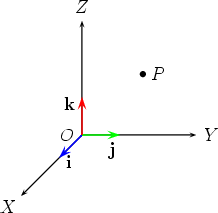
Draw a perpendicular PT from P to the OZ axis. 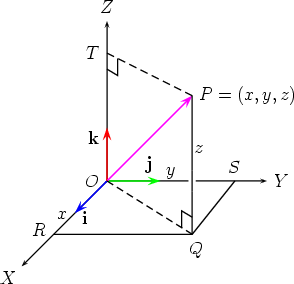
In the rectangle OQPT,PQ and OT both have length z. The vector 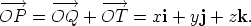
This formula, which expresses The formula 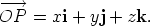 applies in all octants, as x, y and z run through all possible real values.
|
|||||||||||||||||||||||||||||||||||||||||
| Feedback |
|
|||||||||||||||||||||||||||||||||||||||||
© 2002-09 The University of Sydney. Last updated: 09 November 2009
ABN: 15 211 513 464. CRICOS number: 00026A. Phone: +61 2 9351 2222.
Authorised by: Head, School of Mathematics and Statistics.
Contact the University | Disclaimer | Privacy | Accessibility
 is
is  is
is 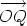 is the sum of
is the sum of 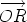 and
and 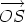 ,
that is,
,
that is,
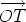 is
is 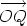
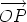 , being the sum of the vectors
, being the sum of the vectors 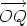 and
and 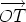 ,
is therefore
,
is therefore
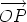 in terms of
in terms of 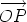 in three dimensions. We call
in three dimensions. We call 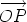 along the
along the